Use quantized data types
High-resolution simulations can deliver great visual quality, but are often limited by the capacity of the onboard memory, GPU memory in particular.
To help reduce the memory footprint of your programs, Taichi provides quantized data types, aka low-precision data types. It allows you to define your own integers, fixed-point numbers, or floating-point numbers with arbitrary number of bits that work best with your limited memory capacity. At the same time, Taichi provides a suite of tailored optimizations to ensure that the runtime performance with quantized data types is comparable to the performance with full-precision data types.
note
For now, quantized data types are supported only on the CPU and CUDA backends.
Quantized data types
Taichi supports the following quantized data types:
- Quantized integers
- Quantized fixed-point numbers
- Quantized floating-point numbers
Quantized integers
Quantized integers in Taichi are represented in the two's complement format but can contain arbitrary number of bits.
- To define a 10-bit signed integer type:
i10 = ti.types.quant.int(bits=10) # `signed` is set to `True` by default
- To define a 5-bit unsigned integer type:
u5 = ti.types.quant.int(bits=5, signed=False)
Quantized fixed-point numbers
The core idea of fixed-point numbers is that, if a specific range is evenly divided into multiple scale units, then a real number within that range can be approximated and represented by multiplying the value of each scale unit by an integer number. Here's an example explaining what the scale unit here is: If you wish to represent a real number within [0, 100] in 10 binary bits, then each scale unit equals 100/210 ≈ 0.098.
Taichi allows you to define quantized fixed-point types of less than 64 bits and with an arbitrary scale unit.
- To define a 10-bit signed fixed-point type within the range [-20.0, 20.0]:
fixed_type_a = ti.types.quant.fixed(bits=10, max_value=20.0) # `signed` is set to `True` by default
- To define a 5-bit unsigned fixed-point type within the range [0.0, 100.0]:
fixed_type_b = ti.types.quant.fixed(bits=5, signed=False, max_value=100.0)
- To define a 6-bit unsigned fixed-point type within [0.0, 64.0]:
fixed_type_c = ti.types.quant.fixed(bits=6, signed=False, scale=1.0) # `scale` is a predefined scaling factor
Set either
scaleormax_value, and Taichi works out the other based on your setting. Do not set both.max_valueis a more commonly used parameter, because you may already know the range of the number to represent.
Quantized floating-point numbers
A floating-point number comprises exponent bits, fraction bits, and a sign bit. There are various floating-point formats:
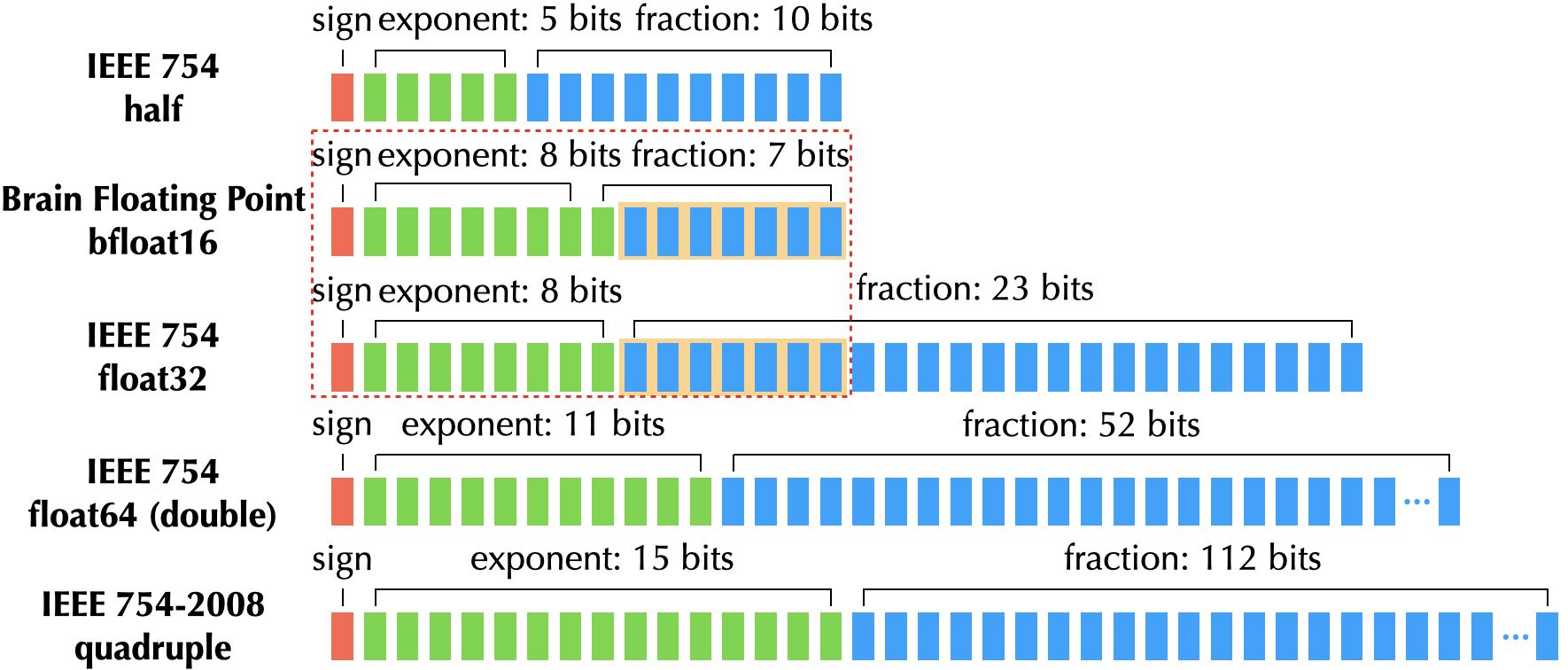
Taichi allows you to define a quantized floating-point number with an arbitrary combination of exponent bits and fraction bits (the sign bit is made part of the fraction bits).
- To define a 15-bit signed floating-point type with five exponent bits:
float_type_a = ti.types.quant.float(exp=5, frac=10) # `signed` is set to `True` by default
- To define a 15-bit unsigned floating-point type with six exponent bits:
float_type_b = ti.types.quant.float(exp=6, frac=9, signed=False)
Compute types
All the above-mentioned parameters specify how a quantized data type is stored in your computer. However, most quantized data types have no native support on hardware, so an actual value of that quantized data type needs to be converted to a primitive type ("compute type") during computation.
- The default compute type for quantized integers is
ti.i32, - The default compute type for quantized fixed-point numbers is
ti.f32, - The default compute type for quantized floating-point numbers is
ti.f32.
To change the compute type of a quantized data type, set the compute parameter when defining the quantized data type:
i21 = ti.types.quant.int(bits=21, compute=ti.i64)
bfloat16 = ti.types.quant.float(exp=8, frac=8, compute=ti.f32)
Data containers for quantized data types
Quantized data types are not primitive types and hence require the following constructs to work with Taichi's data containers.
- Bitpacked fields
- Quant arrays
Bitpacked fields
ti.BitpackedFields packs a group of fields whose dtypes are quantized data types together so that they are stored with one primitive type. You can then place a ti.BitpackedFields instance under any SNode as if each member field is placed individually.
a = ti.field(float_type_a) # 15 bits
b = ti.field(fixed_type_b) # 5 bits
c = ti.field(fixed_type_c) # 6 bits
d = ti.field(u5) # 5 bits
bitpack = ti.BitpackedFields(max_num_bits=32)
bitpack.place(a, b, c, d) # 31 out of 32 bits occupied
ti.root.dense(ti.i, 10).place(bitpack)
Shared exponent
When multiple fields with quantized floating-point types are packed together, there is chance that they can share a common exponent. For example, in a 3D velocity vector, if you know the x-component has a much larger absolute value compared to y- and z-components, then you probably do not care about the exact value of the y- and z-components. In this case, using a shared exponent can leave more bits for components with larger absolute values. You can use place(x, y, z, shared_exponent=True) to make fields x, y, z share a common exponent.
Your first program
You probably cannot wait to write your first Taichi program with quantized data types. The easiest way is to modify the data definitions of an existing example. Assume you want to save memory for examples/simulation/euler.py. Because most data definitions in the example are similar, here only field Q is used for illustration:
N = 16
Q = ti.Vector.field(4, dtype=ti.f32, shape=(N, N))
An element of Q now occupies 4 x 32 = 128 bits. If you can fit it in 64 bits, then the memory usage is halved. A direct and first attempt is to use quantized floating-point numbers with a shared exponent:
float_type_c = ti.types.quant.float(exp=8, frac=14)
Q_old = ti.Vector.field(4, dtype=float_type_c)
bitpack = ti.BitpackedFields(max_num_bits=64)
bitpack.place(Q_old, shared_exponent=True)
ti.root.dense(ti.ij, (N, N)).place(bitpack)
Surprisingly, you find that there is no obvious difference in visual effects after the change, and you now successfully finish a Taichi program with quantized data types! More attempts are left to you.
More complicated quantization schemes
Here comes a more complicated scenario. In a 3D Eulerian fluid simulation, a voxel may need to store a 3D vector for velocity, and an integer value for cell category with three possible values: "source", "Dirichlet boundary", and "Neumann boundar". You can actually store all information with a single 32-bit ti.BitpackedFields:
velocity_component_type = ti.types.quant.float(exp=6, frac=8, compute=ti.f32)
velocity = ti.Vector.field(3, dtype=velocity_component_type)
# Since there are only three cell categories, 2 bits are enough.
cell_category_type = ti.types.quant.int(bits=2, signed=False, compute=ti.i32)
cell_category = ti.field(dtype=cell_category_type)
voxel = ti.BitpackedFields(max_num_bits=32)
# Place three components of velocity into the voxel, and let them share the exponent.
voxel.place(velocity, shared_exponent=True)
# Place the 2-bit cell category.
voxel.place(cell_category)
# Create 512 x 512 x 256 voxels.
ti.root.dense(ti.ijk, (512, 512, 256)).place(voxel)
The compression scheme above allows you to store 13 bytes (4B x 3 + 1B) into just 4 bytes. Note that you can still use velocity and cell_category in the computation code, as if they are ti.f32 and ti.u8.

Quant arrays
Bitpacked fields are actually laid in an array of structure (AOS) order. However, there are also cases where a single quantized type is required to get laid in an array. For example, you may want to store 8 x u4 values in a single u32 type, to represent bin values of a histogram:

Quant array is exactly what you need. A quant_array is a SNode which can reinterpret a primitive type into an array of a quantized type:
bin_value_type = ti.types.quant.int(bits=4, signed=False)
# The quant array for 512 x 512 bin values
array = ti.root.dense(ti.ij, (512, 64)).quant_array(ti.j, 8, max_num_bits=32)
# Place the unsigned 4-bit bin value into the array
array.place(bin_value_type)
note
- Only one field can be placed under a
quant_array. - Only quantized integer types and quantized fixed-point types are supported as the
dtypeof the field under aquant_array. - The size of the
dtypeof the field times the shape of thequant_arraymust be less than or equal to themax_num_bitsof thequant_array.
Bit vectorization
For quant arrays of 1-bit quantized integer types ("boolean"), Taichi provides an additional optimization - bit vectorization. It aims at vectorizing operations on such quant arrays under struct fors:
u1 = ti.types.quant.int(1, False)
N = 512
M = 32
x = ti.field(dtype=u1)
y = ti.field(dtype=u1)
ti.root.dense(ti.i, N // M).quant_array(ti.i, M, max_num_bits=M).place(x)
ti.root.dense(ti.i, N // M).quant_array(ti.i, M, max_num_bits=M).place(y)
@ti.kernel
def assign_vectorized():
ti.loop_config(bit_vectorize=True)
for i, j in x:
y[i, j] = x[i, j] # 32 bits are handled at a time
assign_vectorized()
Reference examples
The following examples are from the QuanTaichi paper, so you can dig into details there.
Game of Life

Eulerian Fluid

MLS-MPM
